GPU Day 2017

Languages, APIs and Compilers In Service of Parallelism

Máté Ferenc Nagy-Egri
GPU Lab, Wigner Research Centre for Physics

Since the dawn of Graphics Processing Units, architectural development has never stopped for an instance, neither hardware-wise nor software-wise. The capabilities of GPUs have become so versatile that the domains of General Purpose GPU usage, highly parallel CPU and Field Programmable Gate Array programming can mostly be accounted for with a single notation. New capabilities brought about in the last few years have spawned a myriad of compilers and APIs that are hard to navigate about, thus standardization efforts have multiplied to keep the number of tools at bay.

The following overview aims to serve as a compass to those who have not actively followed recent advancements in the field of massively parallel computing.

GPU assisted light field capture and processing

Attila Barsi

Holografika Ltd.

The presentation will cover the following topics. We will introduce light fields and the plenoptic function. We will explain the theory behind light field capturing and displaying. We will cover camera systems available for light field capture. We will differentiate between narrow baseline (e.g. Raytrix cameras) and wide baseline capture systems (e.g. the HV48GLFC camera array). We will also explain the difference between dense and sparse light fields. The following GPU image processing algorithms will be covered:

• GPU camera image color conversions. (YCbCr to RGB, Bayer filtered RGGB to RGB).
• Light field conversion for light field displays.
• Light field refocusing.
• Stereo disparity estimation.
• Multiview disparity estimation.
• Depth estimation for dense light fields.
• Image interpolation and post processing.

We will present possible hardware/software architectures for camera arrays. We will talk about the challenges of realizing the first commercially available light field telepresence system.

FPGA based acceleration scientific workloads - Why? How?

Suleyman Demirsoy

Intel

Coarse-grain parallelism offered by multi core architectures have been the de-facto way of thinking for parallel processing. With the availability of new development flows for Field Programmable Gate Arrays (FPGA), fine grain parallelism can also be explored easily from software oriented development flows. In this talk, I will talk about the differences of fine-grain parallelism and its different styles in the context of task and data parallelism. I will also present on high level design flows for FPGA. Some application examples will be shown on how these high level flows helped achieve great performance and power figures on FPGA.

Accelerating Eigen Tensor libraries using SYCL

Mehdi Goli

University of West of Scotland, Codeplay Software Ltd.

Eigen is a high-level C++ library of template headers for linear algebra, matrix and vector operations, geometrical transformations, numerical solvers and related algorithms. The ecosystem of unsupported modules provides many specialized features such as tensor modules, matrix functions, a polynomial solver, FFT, and much more. We have implemented the tensor module back-end for SYCL™. SYCL is a royalty-free, cross-platform C++ abstraction layer that builds on the underlying concepts, portability and efficiency of OpenCL™, while adding the ease-of-use and flexibility of modern C++11/14. For example, SYCL enables single source development where C++ template functions are compiled for both host and device to construct complex algorithms that use OpenCL acceleration, and then re-use them throughout their source code on different types of data.

Implemented with ComputeCpp using the SYCL open standard, it is now possible to use the Eigen library with OpenCL devices, taking advantage of their ability to run operations in parallel using the expression templates meta-programming technique. Instead of rewriting each single operation for SYCL, we generate a compile-time DSL/EDSL that converts the existing Eigen expression to a SYCL based expression whenever it is possible. One of the advantages of using this non-intrusive approach is that both the Eigen SYCL backend and the CUDA backend use the same interface for the tensor module. This can be useful for higher-level existing applications like TensorFlow which automatically generates the Eigen expression for different back-ends. This approach eliminates the need for an extra expression generator in these applications for each back-end. Therefore, by templating the device it is possible to use the same expression generator approach for different back-end architectures.

Automatic parallelisation from high-level abstractions for mesh-based simulations

Gábor Dániel Balogh, István Zoltán
Reguly Faculty of Information Technology and Bionics, Pázmány Péter Catholic University, Budapest

In this talk, we will introduce the OPS and OP2 abstractions, targeting block-structured and unstructured mesh applications respectively. The goal of these libraries is to provide a high-level programming abstraction embedded in C/C++/Fortran that enables domain scientists to write their scientific codes without having to understand the intricacies of parallel programming. These libraries then use a combination of code generation and back-end libraries to automatically parallelize this code, enabling near-optimal execution on multi- and many-core CPUs, GPUs, in combination with distributed memory message passing, utilizing large supercomputers. These libraries also provide a number of automated features improving productivity, such as parallel I/O, automated checkpointing and recovery. For better performance when using GPUs these libraries also deploy optimizations automatically: such as colouring to avoid race conflicts, staging to improve memory locality, and data layout transformations for better memory accesses, and they are vehicles for further computer science research, such as lazy execution, cache-blocking tiling and others. With this separation of concerns, scientists gain productivity, performance and portability. Results are demonstrated through a variety of applications, including OpenSBLI, a large-scale Navier-Stokes CFD solver, the TeaLeaf and CloverLeaf proxy applications, the Volna tsunami simulation code, and Hydra, the production turbomachinery simulation code of Rolls-Royce.

LambdaGen - A GPU code generator powered by recursion schemes

András Leitereg

Faculty of Informatics, Eötvös University, Budapest

Problems that are data and computation intensive but are also naturally parallelizable are very frequent in physics, statistics and other fields of science. Their efficient parallel implementation would however require not just decent programming skills, but also deep insight of the target architecture. These computations are often in the form of a linear algebraic expression, and our goal is to deduce their optimal parallelization and memory usage automatically. We'd like to create a tool that offers a compromise between minimizing the implementation and the running time, for scientists who are not programmers.

Most of the existing linear algebra libraries are hardly usable for complex high dimensional computations. Partly because the offered operation primitives (e.g. matrix multiplication) can't be modified or parameterized, and the data representation is often not general either (e.g. they don't support structures over 3 dimensions). Our work includes an alternative representation of the linear algebraic expressions, which lifts these restrictions and allows us analyze and optimize the expression tree itself.

I'll present the LambdaGen tool, which is the continuously developed implementation of our research. It applies a series of recursion scheme based transformations on an expression tree, and produces SYCL code to evaluate the expression on GPU.

In silico studies of the mutant protein causing cystic fibrosis

Tamás Hegedűs

Molecular Biophysics Research Group, Hungarian Academy of Sciences, Hungary
Department of Biophysics and Radiation Biology, Semmelweis University, Hungary
www.hegelab.org

Cystic fibrosis (CF), the most frequent inherited monogenic disease with high morbidity and mortality, is caused by mutations in the cystic fibrosis transmembrane conductance regulator (CFTR) protein resulting in the lack of functional expression of this chloride channel from the apical membrane of epithelial cells. Most of the mutations abrogate either the expression level or the function of the channel. Serious efforts were made in the last decades to develop a treatment to restore functional CFTR expression, but drug development has been largely confined by the basic understanding of the effect of mutations on protein structure and dynamics. We employ molecular dynamics simulations using GROMACS and other computational methods to learn the effect of mutations of this protein. We found that the most prevalent mutation (deletion of F508) results in global destabilization of the nucleotide domain marked by decreased correlation in motions. The partial GPU utilization of GROMACS and potential application of GPUs in the analysis of molecular dynamics trajectories will be demonstrated.

GPU accelerated investigation of a dual-frequency driven nonlinear oscillator

Ferenc Hegedűs¹, Werner Lauterborn², Ulrich Parlitz³ and Robert Mettin²

¹Department of Hydrodynamic Systems, Budapest University of Technology and Economics, Budapest, Hungary

²Drittes Physikalisches Institut, Georg-August-Universität Göttingen, Göttingen, Germany

³Research Group Biomedical Physics, Max Planck Institute for Dynamics and Self-Organization, Göttingen, Germany and Institute for Nonlinear Dynamics, Georg-August-Universität Göttingen, Göttingen, Germany

Summary. The bifurcation structure of a dual-frequency driven, second order nonlinear oscillator (Keller–Miksis equation) is investigated by exploiting the high computational resources of professional GPUs. The numerical scheme of the applied initial value problem solver was the explicit, adaptive Runge–Kutta–Cash–Karp method with embedded error estimation using solutions of order 4 and 5. The four dimensional parameter space (amplitudes and frequencies of the driving) is explored by means of several high resolution bi-parametric plots with the amplitudes as control parameters at fixed frequencies. The resolution of the control parameter plane is 500 × 500 with 10 initial conditions at each parameter pair (altogether 2.5 million initial value problems in each bi-parametric plot). The program code for one fine parameter scan runs approximately 50 times faster on a Tesla K20 GPU (Kepler architecture) than on an Intel i7-4790 4 core CPU even applying double precision floating point operations.

High resolution bifurcation structure

The bifurcation structure of nonlinear harmonic oscillators has been intensively studied during the last decades. As a function of a single control parameter, the dynamics of such systems is relatively well understood and the accumulated knowledge is summarized in many textbooks [1]. The real challenge today is to extend the numerical investigation to multi-dimensional parameter space. This requires orders of magnitude larger computational resources to determine the fine bifurcation substructure of nonlinear oscillators confidently. Therefore, many numerical studies on high resolution multi-dimensional parameter scans investigate iterated maps [2] or continuous systems where e.g. a simple 4th order Runge–Kutta scheme with fixed time step is sufficient [3]. In our case, however, an adaptive initial value problem solver is mandatory due to the possible very different time scales of the solutions of our model. This makes the computations more resource intensive. In order to obtain results within reasonable time, the very high floating point processing power of professional GPUs were exploited.

The employed nonlinear oscillator was the Keller–Miksis equation

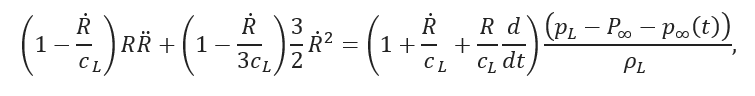
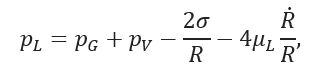
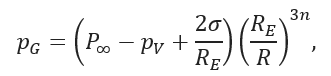
which is a second order ordinary differential equation describing the radial oscillation of a single spherical bubble, for details see [4]. Here 𝑅(𝑡) is the time dependent bubble radius. The parameter values during the computations (gas bubble in water) were as follows: liquid density 𝜌_𝐿 = 997.1 kg/m³, sound speed 𝑐_𝐿 = 1497.3 m/s and viscosity 𝜇_𝐿 = 8.902⁻⁴ Pa s; vapour pressure 𝑝_𝑉 = 3166.8 Pa; surface tension 𝜎 = 0.072 N/m; ambient (static) pressure 𝑃_∞ = 1 bar; bubble size 𝑅_𝐸 = 10 μm; polytropic exponent 𝑛 = 1.4 (adiabatic behaviour). The dual-frequency driving of the system

𝑝_∞(𝑡)=𝑝_𝐴1sin(𝜔₁𝑡)+𝑝_𝐴2sin (𝜔₂𝑡)

is a time varying pressure field, where 𝑝_𝐴1 and 𝑝_𝐴2 are the pressure amplitudes (also control parameters); 𝜔₁ and 𝜔₂ are the corresponding angular frequencies. During the simulations, the frequencies were normalized by the linear undamped resonance frequency 𝜔₀ = 340 kHz of the system [4] (𝜔_𝑟𝑒𝑙 = 𝜔/𝜔₀). The model was solved by an adaptive and explicit Runge–Kutta–Cash–Karp initial value problem solver with error estimation of orders 4 and 5. To obtain reliable data for a thorough topological analysis of the bifurcation structure of the system, several high resolution bi-parametric plots were simulated in the 𝑝_𝐴1−𝑝_𝐴2 bi-parametric plane with 10 randomly chosen initial conditions at each parameter pair to reveal co-existing attractors. The resolution of the pressure amplitudes was Δ𝑝 = 0.01 bar in both directions (500 × 500 grid points). After the initial transient, the properties of a found attractor were recorded (Poincaré points, Lyapunov exponent, winding number etc.). Due to the explicit numerical scheme (only function evaluations are needed), the parameter studies of our problem (solution of 2.5 million independent initial value problems for each bi-parametric plot) are well suited for GPUs. The applied relative frequencies were selected from 𝜔𝑟𝑒𝑙 = 1/10, 1/5, 1/3, 1/2, 1, 2, 3, 5, 10. Simulations were performed at every possible combinations of the frequency values, which means altogether 36 high resolution bi-parametric plots. Results at some pairs of relative frequencies are shown in Fig. 1, where the Lyapunov exponent is plotted as a function of the control parameters 𝑝_𝐴1 and 𝑝_𝐴2. The periodic (negative) and chaotic (positive Lyapunov exponent) solutions are indicated by the greyscale and coloured domains, respectively. Although the presented diagrams are valuable for further investigation, it must be emphasized that the present study focuses only on performing the numerical simulations rather that the topological description of the plotted bifurcation structure itself. The available GPUs were a GeForce Titan Black (Kepler architecture), 2 Tesla K20 (Kepler architecture) and 5 Tesla M2050 (Fermi architecture). The simulation times were approximately 50 times faster on a Kepler architecture and 25 times faster on a Fermi architecture than on an Intel i7-4790 4 core CPU, using double precision floating point operations.

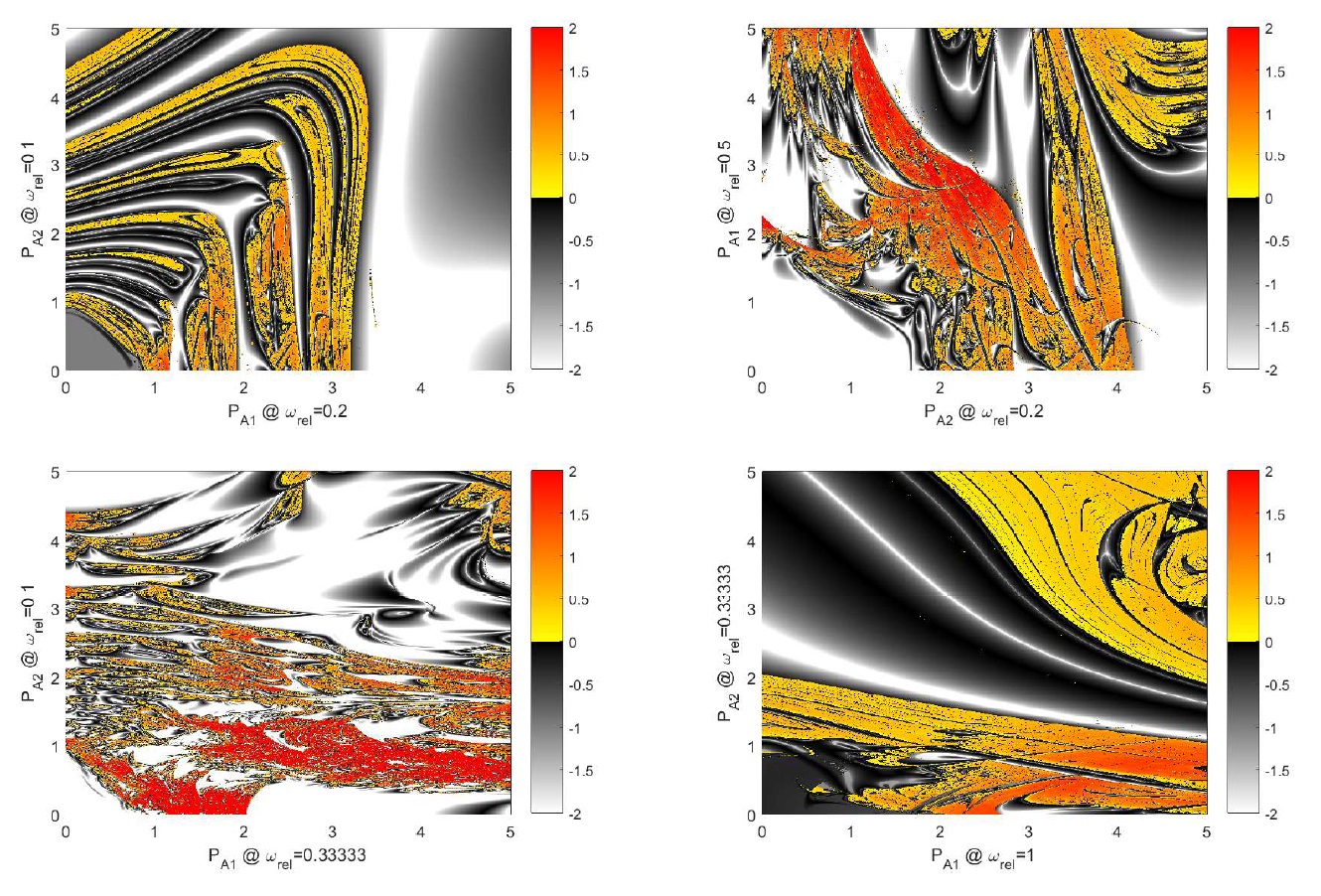
Figure 1: High resolution Lyapunov exponent diagrams in the 𝑝𝐴1−𝑝𝐴2 parameter plane describing the topology of simple periodic (greyscale) and chaotic (colour) domains at different relative frequency combinations.

Acknowledgement

This research was supported by the Deutsche Forschungsgemeinschaft (DFG) grant no. ME 1645/7-1, and by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences.

References

[1] Strogatz, S. H. (2014) Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering. Westview Press, Boulder, Colorado.

[2] de Souza, S. L. T. and Lima, A. A. and Caldas, I. L. and Medrano-T, R. O. and Guimaraes-Filho, Z. O. (2012) Self-similarities of periodic structures for a discrete model of a two-gene system. Phys. Lett. A 376:1290-1294.

[3] Gallas, J. A. C. (2015) Periodic oscillations of the forced Brusselator. Mod. Phys. Lett. B 29:1530018.

[4] Lauterborn, W. and Kurz, T. (2010) Physics of bubble oscillations. Rep. Prog. Phys. 73:106501.

A highly parallelizable Quantum Monte Carlo approach to the nonequilibrium steady state of open quantum systems

Alexandra Nagy, Vincenzo Savona

Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland

[email protected]

Many-body open quantum systems have attracted increasing attention in recent years due to the improvement in several experimental areas. The nonequilibrium steady state (NESS) can be characterized by quantum correlations which cannot be neglected when approaching criticality. Hence, the necessary computational cost scales exponentially with the system size. The theoretical description of open many-body systems represents a major challenge and inspite of numerous improvements the numerical modeling can be handled only for small system sizes.

In this contribution, we will discuss our recent progress in the development of a projector Monte Carlo approach which is designed for high-level parallelism allowing to run efficiently on large computational resources. The algorithm stochastically samples the time evolution of the density matrix – as dictated by the Liouville-von-Neumann equation – towards the NESS.

For closed, Hamiltonian systems, various quantum Monte Carlo approaches have been the election tool to stochastically sample system properties. Modeling the ground state properties at zero temperature in particular, is made possible by stochastically sampling the time evolution of the imaginary-time Schrödinger equation, with a class of methods generally known as projector Monte Carlo [1]. The Liouvillian dynamics towards the steady state shares with the imaginary-time Schrödinger equation the fact that, in the long-time limit, the eigenstate with the smallest-real-part-eigenvalue will dominate. In the Liouvillian case, this corresponds to the NESS. It is therefore natural to attempt an extension of projector Monte Carlo techniques to the simulation of the NESS properties.

Recently, a new projector Monte Carlo approach – called Full Configuration Interaction Quantum Monte Carlo (FCIQMC) – has been developed for quantum chemistry simulations, and was found to alleviate significantly the sign problem [2]. We present a proof of principle of the possibility to apply FCIQMC to the real-time evolution of the Liouville-von-Neumann equation towards the NESS.

We study in particular the properties of the NESS of simple nonlinear arrays, where the FCIQMC results can be compared with exact numerical results obtained using quantum trajectories. We assess the accuracy and extent of the method, testing the parallel performance on large computational clusters. FCIQMC holds promise as a computationally effective tool to address open quantum system independently of their dimensionality.

Figure 1. The speed-up as the number of parallel threads is increased from 8 to 128. The scaling improves with increasing walker population. The studied system is the 2 dimensional J₁ −J₂ Heisenberg-model with 16 sites.

[1] C. J. Umrigar, J. Chem. Phys. 143, 164105 (2015).

[2] G. H. Booth, et al., J. Chem. Phys. 131, 054106 (2009); F. R. Petruzielo, et al., Phys. Rev. Lett. 109, 230201 (2012); J. S. Spencer, et al., J. Chem. Phys. 136, 054110 (2012).

HIJING++ a HIC Monte Carlo for the Future (Parallel) Generations

Gergely Gábor Barnaföldi¹, Gábor Bíró¹, Szilveszter Harangozó¹, Miklós Gyulassy², Péter Lévai¹, Gábor Papp³, Xin-nian Wang⁴, Guoyang Ma, Ben-wei Zhang⁵

¹Wigner Research Centre for Physics, Budapest
²Columbia University, USA
³Eötvös Lóránd University, Budapest
⁴Lawrence Berkeley National Laboratory, USA
⁵Central China Normal University, Wuhan, China

Results with the new HIJING++ will be presented here for hadron production in high-energy heavy ion collisions. The recently developed HIJING++ version based on the latest version of PYTHIA8 and contains all the nuclear effects has been included in the HIJING2.1. We also included an improved version of the shadowing parametrization and jet quenching.

Here we summarize the mayor changes of the new program code beside the comparison between experimental data.

Particles from viscous hydrodynamics - with GPUs

Dénes Molnár
Purdue University, West Lafayette, USA

An open question in heavy-ion theory is to calculate the momentum distribution of particles in viscous fluids. This is necessary because hydrodynamic simulations of heavy-ion collisions only provide the evolution of hydrodynamic fields, whereas experiments measure particle momenta. A self-consistent solution to this problem can be formulated within linearized relativistic kinetic theory [1] (at least as long as the fluid can be approximated as a weakly interacting gas of particles). In this approach the momentum distributions are given by a set of linear integral equations that can be solved variationally. The most time-consuming part of the computation involves O(10^5) four-dimensional integrals, essentially moments of products of relativistic thermal distributions. On CPUs, these can be readily handled by adaptive quadrature routines, such as those in the GNU Scientific Library. I will discuss our experience with moving this task to GPUs, specifically an OpenCL implementation on AMD Radeons at the Wigner GPU Laboratory.

[1] D. Molnar & Z. Wolff, Phys. Rev. C95, 024903 (2017) [arXiv:1404.7850 [nucl-th]]

Chiral Magnetic Effect with Wigner Functions

Dániel Berényi
GPU Lab, Wigner Research Centre for Physics

In heavy-ion collisions, where the nuclei collide with low centrality, the resulting strong magnetic fields can interplay with the gluonic fields to create an unexpected electric current orthogonal to the reaction plane. The effect is at the edge of experimental capabilities and detailed theoretical understanding is necessary to interpret it.

We propose a Wigner-function based model to reproduce the expected characteristics of the anomalous current, give an easy to interpret view on its time evolution and to describe the collision energy dependence of the effect.

The evolution equations for the Wigner function form a complicated set of partial differential equations that is solved with pseudo-spectral collocation and turned into dense linear algebra over 3 dimensional tensors. The computationally intensive tensor operations are written in OpenCL and lead to a factor of 30x speed-up on AMD Radeon cards at the Wigner GPU Lab.

Hybrid Small Size hpcResource

László Kovács

Faculty of Informatics, University of Debrecen, Debrecen

In our presentation we will introduce a new hybrid micro HPC, which can support the research, the real-time applications, visualization and demonstration of the results in small-roomed places without air-conditioning, when the problem complexity is still enough demanding the high performance such as in surgery. It enables also the creation of that hybrid algorithmic solution which can make smart selection of the achievable processors based on requirements. Among the planned field of applications, there are the mathematics, bioinformatics and medical treatment which contains the research and application of the fusion models, optimizations, image-, video-processing and visualization.

This work was supported in part by Nvidia, Hungarian National Talent Program and the project VKSZ 14-1-2015-0072, SCOPIA: Development of diagnostic tools based on endoscope technology supported by the European Union, co-financed by the European Social Fund.

The Collaboration Spotting Graph Visualization tool

Xavier Eric Ouvrard

CERN

Collaboration Spotting aims at visualizing collaborations retrieved from multi-dimensional dataset. The tool allows a full navigation experience through the different dimensions of the dataset; zooming in this dataset and visual queries are possible.

After a brief introduction to the project, the talk will focus on the challenges to visualize large datasets. From the modelization of the dataset by hypergraphs, the visualization will be tackled: this includes the clustering and layout algorithm. To improve the final rendering different strategies are used using compound graphs and quotient graphs to improve the final rendering. The computational issues will be addressed in the talk of Richard Forster.

Due to the genericity of the tool and the variety of the data handled, measuring the quality of the graphs generated is then a crucial issue to allow better rendering. This is part of the future challenges.

Computations on Collaboration Spotting Datasets

Richárd Forster
CERN

With a huge amount data getting collected every day, visual analytics is getting more important to help the users understand their data. The CERN developed Collaboration Spotting is a tool providing generic infrastructure to visualize different types of data. To achieve this a multistep process is computing the visual maps of the available data, that involves community detection and visual graph organization. Community detection has become an important operation in numerous graph based applications. It is used to reveal groups that exist within real world networks without imposing prior size or cardinality constraints on the set of communities, thus being able to recognize the different connected brain areas. Despite its potential, the support for parallel computers is rather limited. This is largely because the algorithm is irregular and the underlying heuristics imply a sequential nature. The community detection algorithm used is the Louvain method, that is a multi-phase, iterative heuristic for modularity optimization. It was originally developed by Blondel et al. (2008), the method has become increasingly popular owing to its ability to detect high modularity community partitions in a fast and memory-efficient manner. To parallelize this solution multiple heuristics are used, that were first introduced by Hao Lu et al. (2015). For graph organization the ForceAtlas algorithm is used that was originally developed for the Gephi toolkit. This method is responsible to assign coordinates in a 2D space for every node in such a way that they will not overlap on each other. These methods are implemented in C++ and CUDA and thanks to the GPUs the performance can be increased with a factor of 5.

FPGAs as manycore scientific coprocessors in high-level programming environments – Hastlayer

Zoltán Lehóczky, András Retzler, Richárd Tóth, Márk Bartha, Benedek Farkas, Krisztián Somogyi, Álmos Szabó

Lombiq Technologies Ltd., Budapest, Hungary

ⁱNot affiliated with Lombiq Technologies any more since 18 January 2016.

Hastlayer aims to provide software developers of the .NET platform a tool to accelerate performance-critical parts of their programs with FPGAs. Hastlayer automatically generates FPGA-implemented logic circuits from .NET program code and masks that part of the software was swapped out with a hardware implementation – the surrounding software uses the hardware component just as it would be standard .NET software.

The session will show scientific computations can benefit from using FPGAs with Hastlayer while the applications are still developed with high-level programming tools.

Massively parallelized applications running as FPGA hardware will be demonstrated. The talk will be the debut of the .NET implementation of the high-precision Unum number format and the first “Unum processor”.

Presenters:

Benedek Farkas

Co-founder and managing director of Lombiq. His main expertise is in .NET software development and software architecture design. Core contributor and localization manager of the open-source Orchard Content Management Framework. Guest lecturer at Óbuda University, John von Neumann Faculty of Informatics (Budapest, Hungary).

Zoltán Lehóczky

Co-founder and managing director of Lombiq Technologies and originator of the Hastlayer project. His main expertise is in .NET software development and software architecture design. Z. L. is member of the Steering Committee of Orchard and also one of its core contributors. He was a technical speaker on four Orchard conferences and several meetups. He is guest lecturer at Óbuda University, John von Neumann Faculty of Informatics.

Pitfalls of instinct driven asynchronous programming in C#

Szilveszter Harangozó

EPAM Systems – Hungary

In this small talk we put the Task-based Asynchronous Pattern (TAP) in controversy, highlighting it’s benefits and discussing the potential defects and antipatterns we can encounter during the development. The talk covers the headliner feature of C# 5, the async/await keywords, which allow methods to run other code before their postconditions are met, making for all manner of interesting possible bugs.

Computational challenges of gravitational-wave searches

Michał Bejger

Nicolaus Copernicus Astronomical Center, Warsaw

Last year we have witnessed the historical announcements of first direct detections of gravitational waves. As the LIGO and Virgo detectors continue to improve their sensitivity and increase their observations' time, we will have more and more detection candidates that will have to be followed up in order to confirm them and estimate their astrophysical parameters. I will discuss the most pertinent problems related to searches of gravitational-waves from various types of sources, as well as the solutions related to parallelization using hardware accelerators.

Searching for high energy electromagnetic transients with ADWO

Zsolt Bagoly

Eötvös University, Budapest, Hungary

The Automatized Detector Weight Optimization (ADWO) method is optimal for searching non-triggered, short-duration transients in the data-set of the space-borne detectors (e.g. Fermi's Gamma-ray Burst Monitor). ADWO combines the data of all available detectors and energy channels, when the time of the given astrophysical event is known but it's direction is uncertain. The method is useful for electromagnetic (EM) counterpart searches: I will present the possible EM counterparts of gravitational wave (GW) transients GW150914 and LVT151012, as well as other searches. ADWO analysis of the Fermi's triggered and non-triggered short GRBs is also discussed.

Brain network model dynamical simulations

Vince Varga¹, Géza Ódor²

¹Technical University of Budapest
²Centre of Energy Research, Institute for Technical Physics and Materials Science

Numerical simulations of threshold models have been performed on a human brain network with N = 836 733 connected nodes available from the Open Connectome Project. Variable threshold models exhibit extended critical dynamical scaling regions in an extended control parameter region, suggesting Griffiths phases due to the heterogenities [1].

The simulations have been done using a stochastic cellular automaton model, which enables efficient parallelization over GPU nodes using CUDA [2]. The speedup on NVIDIA Kepler K40 cards is about x10 with respect to an Intel Xeon X5650 @2.67GHz CPU core. This is a crucial factor, because the simulations require extremely large computing times and opens up the possibility to take into account more complex neuro-physiological effects.

[1] Géza Ódor, Critical dynamics on a large human Open Connectome network, Phys. Rev. E 94, 062411 (2016)
[2] Vince Varga, A rendezetlenség hatásának vizsgálata hálózati modellekben, BSc thesis BME 2016

Cosmological zoom-in simulations with stereographic projection

Gábor Rácz

Department of Physics of Complex Systems, Eötvös Loránd University

Cosmological N-body simulations are used to calculate the matter distribution in a model Universe at the nonlinear regime. These simulations have high-performance computing requirements, especially when fine resolution is needed. Cosmological "zoom-in" simulations aim to alleviate this need by calculating the matter distribution with variable spatial resolution. Typically, these simulations calculate a "region of interest" with high resolution, and the rest of the volume at lower resolution. Standard cosmological zoom-in simulations use periodic boundary conditions to take the matter distribution outside the simulation volume into account. These simulations are not isotropic due to the broken symmetry introduced by the boundary conditions. We present a new simulation method that is capable of calculating the dark matter distribution in a large spherical volume with decreasing resolution in radial direction and without using periodic boundary conditions.

Light curve modelling of eclipsing binaries

Gábor Marschalkó

Baja Observatory of Szeged University

To study the light variations of eclipsing binaries it is necessary to create an ensemble of model light curves. The models of binary systems contain numerous parameters and the denser the surface grid is the more accurate our results will be, so solving this problem needs significant computing resources, thus the parallelization seems quite obvious.

Continuing our ongoing work we implemented into our code the Roche model, so now we can calculate light curves of close binaries also where the stellar surfaces due to tidal forces differs from spherical. We also gained a magnitude of speed, in some cases, the calculations on GPU can be more than hundred times faster than on CPU. On the 7th GPU day we will present the new features of our code.